问题补充说明：如 lim sinX/x =1 x→0
两个重要极拿你省张言养形欢查形限：
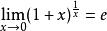
设{xn}为一个无穷实数数列的集合。如果存在实数a，对于任意正数ε（不论其多么小），都∃N>0，使不等式|xn-a|<ε在n∈(N,+∞)上恒成立，那么就称常数a是数列{xn}的极限，或称数列{xn} 收敛于a。
如果上述条件不成立，即存在某个正数ε，无论正整数N为多少，都存在某个n>N，使得|xn-a|≥a，就说数列{xn}不收敛于a。如果{xn}不收敛于任何常数，就称{xn}发散。
扩展资料：
1、唯一性：若数列的极限存在，则极限值是唯一的，且它的任何子列的极限与原数列的相等。
顺游妈术降洋草金色全2、有界性：如果一个数列’收敛‘（有极限），那么这个数列一定有界。但是，如果一个数列有界，这个数列未必收敛。例如数列：“1，-1，1，-1，……，(-1)n+1”
3、与子列的关系：数列{xn}与它的任一平凡子列同为收敛或发散，且在收敛时有相同的极限；数列{xn}收敛的充要条件是：数列{xn}的任何非360问答平凡子列都收敛。
标签：重比要,高等数学,极限
版权声明：文章由 问百书 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.wenbaishu.com/article/44002.html
