张量(tensor)理论是数学的一个分支学科,是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数,在力学中有重要应用。
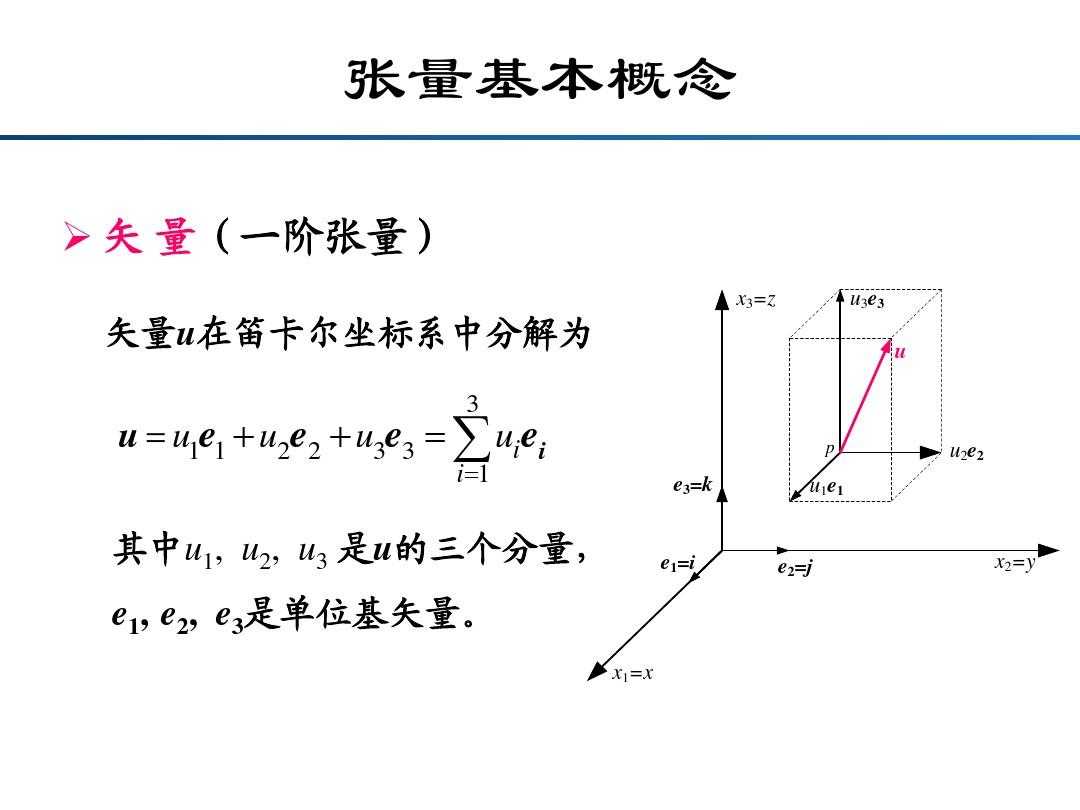
张量这一术语起源于力学,它最初是用来表示弹性介质中各点应力状态的,后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要,在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广,矢量是一阶张量。
张量(Tensor)是一个定义在一些向量空间和一些对偶空间的笛卡儿积上的多重线性映射,其坐标是|n|维空间内,有|n|个含档分量的一种量, 其中每个分量都是坐标的函数, 而在坐标变换时,这些分量也依照某些规则作线性变换。r 称为该张量的秩或阶(与矩阵的秩和阶均无关系)。
在同构的意义下,第零阶张量 (r = 0) 为标量 (Scalar),第一阶张量 (r = 1) 为向量 (Vector), 第二阶张量 (r = 2) 则成为矩阵 (Matrix)。例如,对于3维空间,r=1时的张量为此向量:(x,y,z)。
由于变换方式的不同,张量分成协变张量 (Covariant Tensor,指标在下者)、逆变张量 (Contravariant Tensor,指标在上者)、 混合张量 (指标在上和指标在下两者都有) 三类。
扩展资料
基本运算
1、加减法
两个或多个同阶同型张量之和(差)仍是与它们同阶同型的张量。
2、并积
两个张量的并积是一个阶数等于原来两个张量阶数之和的新张量。
3、缩并
使张量的一个上标和一个下标相同的运算,其结果是一个比原来张量低二阶的新张量。
4、点积
两个张量之间并积和缩并的联合运算。例如,在极分解定理中,三个二阶张量R、U和V中一次点积R·U和V·R的结果是二阶张量F。
5、对称化和反称化
对已给张量的n个指标进行n1不同置换并取所昌老链得的n1个新张量的算术平均值的运算称为对称化耐孙。把指标经过奇次置换的新张量取反符号后再求算术平均值的运算称为反称化。
参考资料:百度百科——张量
标签:张量