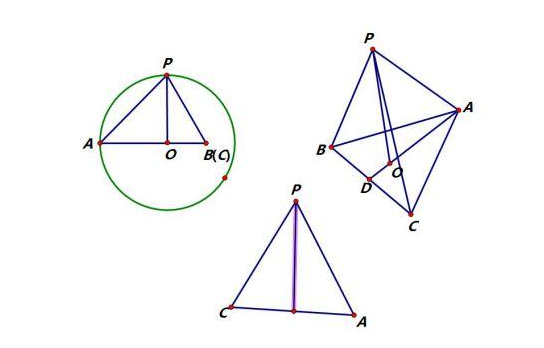
正三棱锥的外接球半径求法:
设A-BCD是正三棱锥,侧棱长为a,底面边长为b,则外接球的球心一定在这个三棱锥的高上。
设高为AM,连接DM交BC于E,连接AE,然后在面ADE内做侧棱AD的垂直平分线交三棱锥的高AM于O,则0就是外接球的球心,AO,DO是外接球的半径。
(当三棱锥的侧棱与它的对面所成的线面角小于90度时,即角DAE小于90度时,球心在棱锥的内部;当线面角等于90度时,球心恰好在底面正三角形的中心M上。
当线面角大于90度时,球心在棱锥的外部,在棱锥高AM的延长线。下面我给出的解法是第一种情况,球心在棱锥的内部。另缺闭两种情况你自己可以照理推出。)
设AO=DO=R
则,DM=2/3DE=2/3*2分之根号3倍的b=b/根号3
AM=根号(a^2-b^2/3)
OM=AM-A0=根号(a^2-b^2/3)-R
由DO^2=OM^2+DM^2得
R=根号3倍的a^2÷2倍的根号(3a^2-b^2)
内切球半径用等体积法,连接内切球球心和棱锥各顶点分割成若干三棱锥,则每个三棱锥体积为1/3底面积×R,全棱锥体积为1/3全面积×R;外接球则先考查任一侧面的三点外心的法线;对于特殊棱锥考迟腊虑补形为长方体之类的。
扩展资料
三棱锥外接球又是主要的一种,主要是能补成长方体(包括正方体、正四棱锥)的三棱锥、侧棱与底面垂直的三棱锥、底面与底面垂直的三棱锥和正三棱锥。
补形的类型有:
类型1:一个顶点上三条棱互相垂直,由以互相垂直的三条棱为长、宽、高补成一个长方体,此时长方体的对角线就是外接球直径。
类型2:三组对棱分别相等的三棱锥,此时以对棱为相对面的对角线补成一个长方体
类型3:两组对棱都相等的三棱锥,另一组对棱也相等的三棱锥,可补成正四棱柱
类型4:正四面体(即各棱都相等的三棱锥)。码扮滑以棱长为正方体面的对角线补成正方体。
标签:三棱锥,接球,半径