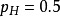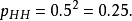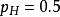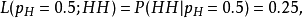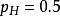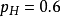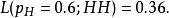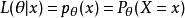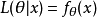数理统计中似然函数怎么求啊

考虑投掷一枚硬币的实验。假如已知投出的硬币正面朝上的概率是

便可以知道投掷若干次后出现各种结果的可能性。比如说，投两次都是正面朝上的概率是0.25：

从另一个角度上说，给定“投两次都是正面朝上”的观测，则硬币正面朝上的概率为0.5的似然是

尽管这并不表示当观测到两次正面朝上时

的“概率”0.25。如果考虑

那么似然函数的值会变大

这说明，如果参数的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设0.5 时更大。也就是说，参州汪数取成0.6 要比取成0.5 更有说服力，更为“合理”。

总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到搭迹困最大的话，那么这个值就是最为“合理”的参数值。 

数理统计中似然函数的分布类型：

1、离散型概率分布

假定一个关于参数θ、具有离散型概率分布P的随机变量X，则在给定X的输出x时，参数θ的似然函数可表示为

需要注意的是，此处并非条件概率，因为θ不（总）是随机变量。

2、连续型概率分布

假定一个关于参数θ、具有连续概率密度函数f的随机变量X，则在给定X的输出x时，参数θ的似然函数可表示知念为

似然函数的主要用法在于比较它相对取值，虽然这个数值本身不具备任何含义。

似然函数乘以一个正的常数之后仍然是似然函数，其取值并不需要满足归一化条件

似然函数的这种特性还允许我们叠加计算一组具备相同含义的参数的独立同分布样本的似然函数。

关于利用似然函数进行统计推断的应用，可以参考最大似然估计（Maximum likelihood estimation）方法和似然比检验（Likelihood-ratio testing）方法。

参考资料来源：百度百科-似然函数

标签：似然,数理统计,函数